2019 AMC 10A 试题/第1题
第1题
求下列表达式的值
\[ {2}^{\left( {0}^{\left( {1}^{9}\right) }\right) } + {\left( {\left( {2}^{0}\right) }^{1}\right) }^{9}\text{?} \]
\( \textbf{(A)}\;0\;\textbf{(B)}\;1\;\textbf{(C)}\;2\;\textbf{(D)}\;3\;\textbf{(E)}\;4 \) 解答 \( {2}^{\left( {0}^{\left( {1}^{9}\right) }\right) } + {\left( {\left( {2}^{0}\right) }^{1}\right) }^{9} \) 
2019 AMC 10A 试题/第2题
题目
\( \left( {{20}! - {15}!}\right) \) 的百位数字是多少?
(A) 0 (B) 1 (C) 2 (D) 4 (E) 5
解答
对于所有 \( n \geq {15} \) , \( n! \) 的最后三位都是000,因为其质因数分解中至少有三个2和三个5。由于 \( 0 - 0 = 0 \) ,故答案为 (A) 0
2019 AMC 10A 试题/第3题
题目
Ana 和 Bonita 出生在同一天,但年份相差 \( n \) 岁。去年 Ana 的年龄是 Bonita 的5倍;今年 Ana 的年龄是 Bonita 年龄的平方。求 \( n? \)
(A) 3 (B) 5 (C) 9 (D) 12 (E) 15
解答
解法1
设 \( A \) 为Ana的年龄, \( B \) 为Bonita的年龄。那么,
且
\[ A = {B}^{2}. \]
将第二个方程代入第一个方程,我们得到
\[ {B}^{2} - 1 = 5\left( {B - 1}\right) \text{.} \]
利用平方差公式并约分, \( B = 4. \) 此外, \( A = {B}^{2} = {16}. \) 答案是
解法2(猜测与验证)
简单的猜测与验证即可。从所有平方数减1开始:1,4,9,16,25等(大约到100即可,再大就不合理了)。若Ana为9岁,则Bonita为3岁,于是前一年Ana的年龄是Bonita的4倍。若Ana为16岁,则Bonita为4岁,且前一年Ana的年龄是Bonita的5倍,符合题意。两人年龄差为 \( {16} - 4 = {12} \) 。(D)
解法3(选项法)
题中第二句说Ana的年龄曾是Bonita的5倍,因此年龄差 \( n \) 必须能被4整除。唯一能被4整除的选项是 \( {12} \rightarrow \left( D\right) \) 。
- awesome_weisur
- 一个正方形
- 一个非正方形的矩形
- 一个不是正方形的菱形
- 一个既不是矩形也不是菱形的平行四边形
2019 AMC 10A 第4题
以下题目同时出现在2019 AMC 10A第4题和2019 AMC 12A第3题,因此两题均重定向至此页面。
题目
一个盒子里有28个红球、20个绿球、19个黄球、13个蓝球、11个白球和9个黑球。最少需要从中不放回地取出多少个球,才能保证至少取到15个同色球?
(A) 75 (B) 76 (C) 79 (D) 84 (E) 91
解答
若每种颜色都取到 \( < {15} \) 个球,最多可取14个红球、14个绿球、14个黄球、13个蓝球、11个白球和9个黑球,共75个球。再取1个球,就能保证至少得到15个同色球——红、绿或黄。因此答案为
\( {75} + 1 = 0 \) (B) 76.
2019年AMC 10A试题/第5题
问题
连续整数之和等于 \( {45}? \) 的最大个数是多少?
(A) 9 (B) 25 (C) 45 (D) 90 (E) 120 解法1
我们起初可能会认为答案是9,因为 \( 1 + 2 + 3\cdots + n = {45} \) 当 \( n = 9 \) 。但请注意,题目说的是它们可以是整数,而不一定是正整数。同时还可观察到,序列 \( \underline{-{44}, - {43},\cdots ,{44},{45}} \) 中除45外的所有项都相互抵消。因此,直观地看,答案是(D) 90个整数。
尽管不切实际,但最大性的证明可如下进行:设所求的连续整数序列为 \( a, a + 1,\cdots , a + \left( {N - 1}\right) \) ,其中共有 \( N \) 项,我们希望最大化 \( N \) 。于是该序列各项之和为 \( {aN} + \frac{\left( {N - 1}\right) \left( N\right) }{2} = {45} \) 。经整理并因式分解,问题化为 \( N\left( {{2a} + N - 1}\right) = {90} \) 。由于 \( N \) 必须整除90,且已知90是可达到的和,故90必为最大值。解法2
为了使整数数量最大化,我们需要让它们的平均值尽可能低,但仍保持为正。若中间两个数为0和1,则平均值可为 \( \frac{1}{2} \) ,因此答案为 \( \frac{45}{\frac{1}{2}} = \) (D)90
2019年AMC 10A试题/第6题
问题
对于以下四边形类型中的多少种,存在位于该四边形所在平面内且到四个顶点距离均相等的点?
一个不是平行四边形的等腰梯形
(A) 0 (B) 2 (C) 3 (D) 4
解法1
这道题只是在问列出的四边形中有多少个是圆内接四边形(cyclic quadrilateral)(因为与四个顶点等距的点就是外接圆的圆心)。正方形、矩形以及非平行四边形的等腰梯形都是圆内接四边形,其余两种不是。因此答案是 \( \left| {\left( \mathbf{C}\right) \text{ 3 }}\right| \)
我们只需检查对角之和是否为180度~Williamgolly
解法2
我们可以用排除法。依次查看,正方形显然满足;非正方形的矩形也满足。菱形和平行四边形都没有与四个顶点等距的点,但等腰梯形有,所以答案是 \( \left( \mathbf{C}\right) 3 \) 。
解法3
线段的垂直平分线是与两端点等距的所有点的轨迹。问题于是转化为寻找那些各边垂直平分线交于一点的图形。正方形、矩形和等腰梯形都满足,因此答案是(C) 3
解法4
只有圆内接四边形(cyclic quadrilateral)才符合描述(它们 \( R \) )。逐一检查后,答案是 \( \left| {\mathbf{C}\mathbf{C}3}\right| \) 。
-JoshBrother32
2019 AMC 10A 试题/第7题
题目
两条斜率分别为 \( \frac{1}{2} \) 和2的直线在(2,2)相交。这两条直线与直线 \( x + y = {10} \) 围成的三角形面积是多少?
(A) 4 (B) \( 4\sqrt{2} \) (C) 6 (D) 8 (E) \( 6\sqrt{2} \)
解法1
先把三条直线写成斜截式: \( \left( {x, y}\right) = \left( {2,2}\right) \) 和 \( y = \frac{x}{2} + b \) 得 \( 2 = \frac{2}{2} + b = 1 + b \) ,故 \( b = 1 \) ; \( y = {2x} + c \) 得 \( 2 = \bar{2} \cdot 2 + c = 4 + c \) ,故 \( c = - 2 \) 。又 \( x + y = {10} \) 得 \( y = - x + {10} \) 。于是三条直线为 \( y = \frac{x}{2} + 1, y = {2x} - 2, \) 和 \( y = - x + {10} \) 。再求它们与 \( y = - x + {10} \) 的交点,得(6,4)和(4,6)。用距离公式和勾股定理可知这是一个等腰三角形,底边 \( 2\sqrt{2} \) ,高 \( 3\sqrt{2} \) ,面积为 \( 1\mathrm{\left( C\right) }6 \) 。
解法2
与解法1相同,我们确定三角形三个顶点的坐标。得到的坐标为: \( \left( {2,2}\right) \left( {6,4}\right) \left( {4,6}\right) \) 。现在,利用鞋带定理(Shoelace Theorem),可直接求得面积为 \( \left( \mathbf{C}\right) 6 \) 。
解法3
与其他解法一样,解方程组可知三角形的另外两个顶点位于(4,6)和(6,4)。然后应用海伦公式(Heron’s Formula):半周长为 \( s = \sqrt{2} + \sqrt{20} \) ,于是面积恰好化简为平方差,结果为
解法4
与其他解法相同,我们利用代数方法或直接在方格纸上画线,得到三个交点(2,2)、(4,6)和(6,4)。现在可画出外接正方形,其顶点为(2,2)、(2,6)、(6,6)和(6,2),从而推得三角形面积为 \( {16} - 4 - 2 - 4 = \mathrm{O} \) 。
解法5
与其他解法一样,我们得到三个交点(2,2)、(4,6)和(6,4)。在方格纸上可见,该三角形有6个边界格点和4个内部格点。根据皮克定理(Pick’s Theorem),面积为 \( \frac{6}{2} + 4 - 1 = 0 \) (C) 6
解法6
与其他解法相同,我们求出三个交点。将它们标记为 \( A\left( {2,2}\right) \) 、 \( B\left( {4,6}\right) \) 和 \( C\left( {6,4}\right) \) 。根据勾股定理(Pythagorean Theorem), \( {AB} = {AC} = 2\sqrt{5} \) 且 \( {BC} = 2\sqrt{2} \) 。再由余弦定理(Law of Cosines),
\[ \cos A = \frac{{\left( 2\sqrt{5}\right) }^{2} + {\left( 2\sqrt{5}\right) }^{2} - {\left( 2\sqrt{2}\right) }^{2}}{2 \cdot 2\sqrt{5} \cdot 2\sqrt{5}} = \frac{{20} + {20} - 8}{40} = \frac{32}{40} = \frac{4}{5} \]
因此, \( \sin A = \sqrt{1 - {\cos }^{2}A} = \frac{3}{5} \) ,于是面积为
\( \frac{1}{2}{bc}\sin A = \frac{1}{2} \cdot 2\sqrt{5} \cdot 2\sqrt{5} \cdot \frac{3}{5} = \) (C)6.
解法7
与其他解法一样,我们得到三个交点(2,2)、(4,6)和(6,4)。三角形面积等于由这些点构成的矩阵的行列式绝对值的一半。
\[ \frac{1}{2}\begin{Vmatrix} 2 & 2 & 1 \\ 4 & 6 & 1 \\ 6 & 4 & 1 \end{Vmatrix} = \frac{1}{2}\left| {-{12}}\right| = \frac{1}{2} \cdot {12} = 1 \]
解法8
与其他解法相同,我们求出三个交点。将它们标记为 \( A\left( {2,2}\right) \) 、 \( B\left( {4,6}\right) \) 和 \( C\left( {6,4}\right) \) 。则向量 \( \overrightarrow{AB} = \langle 2,4\rangle \) 和 \( \overrightarrow{AC} = \langle 4,2\rangle \) 。三角形面积等于这两个向量叉积模的一半。
\[ \frac{1}{2}\begin{Vmatrix} i & j & k \\ 2 & 4 & 0 \\ 4 & 2 & 0 \end{Vmatrix} = \frac{1}{2}\left| {-{12k}}\right| = \frac{1}{2} \cdot {12} = 1 \]
解法9
与其他解法一样,我们求得三个交点为(2,2)、 \( \left( {\underline{4},6}\right) \) 和(6,4)。根据勾股定理(Pythagorean theorem),这是一个等腰三角形,底边为 \( 2\sqrt{2} \) ,两腰长均为 \( 2\sqrt{5} \) 。底边为 \( b \) 、两腰长为 \( l \) 的等腰三角形面积为 \( \frac{b\sqrt{4{l}^{2} - {b}^{2}}}{4} \) 。代入 \( b = 2\sqrt{2} \) 和 \( l = 2\sqrt{5} \) ,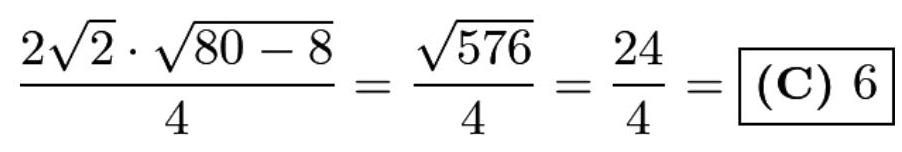
解法10(三角法)
与其他解法一样,我们求出三个交点,记为 \( A\left( {2,2}\right) \) 、 \( B\left( {4,6}\right) \) 和 \( C\left( {6,4}\right) \) 。根据勾股定理(Pythagorean Theorem), \( {AB} = {AC} = 2\sqrt{5} \) 且 \( {BC} = 2\sqrt{2} \) 。由余弦定理(Law of Cosines),
\[ \cos A = \frac{{\left( 2\sqrt{5}\right) }^{2} + {\left( 2\sqrt{5}\right) }^{2} - {\left( 2\sqrt{2}\right) }^{2}}{2 \cdot 2\sqrt{5} \cdot 2\sqrt{5}} = \frac{{20} + {20} - 8}{40} = \frac{32}{40} = \frac{4}{5} \]
因此, \( \sin A = \sqrt{1 - {\cos }^{2}A} = \frac{3}{5} \) 。根据扩展正弦定理(extended Law of Sines),
\[ {2R} = \frac{a}{\sin A} = \frac{2\sqrt{2}}{\frac{3}{5}} = \frac{{10}\sqrt{2}}{3} \]
\[ R = \frac{5\sqrt{2}}{3} \]
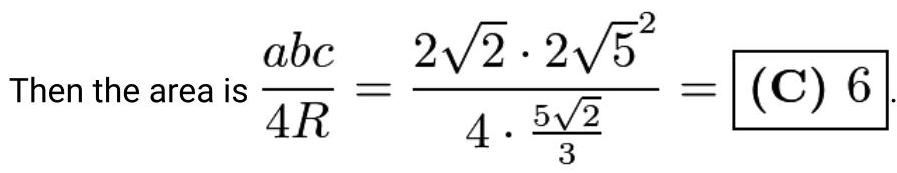
解法11
由三条直线围成的三角形面积
\[ {a}_{1}x + {a}_{2}y + {a}_{3} = 0 \]
\[ {b}_{1}x + {b}_{2}y + {b}_{3} = 0 \]
\[ {c}_{1}x + {c}_{2}y + {c}_{3} = 0 \]
等于以下表达式的绝对值
\[ \frac{1}{2} \cdot \frac{1}{\left( {{b}_{1}{c}_{2} - {b}_{2}{c}_{1}}\right) \left( {{a}_{1}{c}_{2} - {a}_{2}{c}_{1}}\right) \left( {{a}_{1}{b}_{2} - {a}_{2}{b}_{1}}\right) } \cdot {\left| \begin{array}{lll} {a}_{1} & {a}_{2} & {a}_{3} \\ {b}_{1} & {b}_{2} & {b}_{3} \\ {c}_{1} & {c}_{2} & {c}_{3} \end{array}\right| }^{2} \]
代入这三条直线,
\[ - x + {2y} - 2 = 0 \]
\[ - {2x} + y + 2 = 0 \]
\[ x + y - {10} = 0 \]
面积等于以下表达式的绝对值
\[ \frac{1}{2} \cdot \frac{1}{\left( {-2 - 1}\right) \left( {-1 - 2}\right) \left( {-1 + 4}\right) } \cdot {\left| \begin{matrix} - 1 & 2 & - 2 \\ - 2 & 1 & 2 \\ 1 & 1 & - {10} \end{matrix}\right| }^{2} = \frac{1}{2} \cdot \frac{1}{27} \cdot {18}^{2} = 1\left( \mathbf{C}\right) 6 \]
2019 AMC 10A 试题/第8题
以下题目同时出现在2019 AMC 10A第8题和2019 AMC 12A第6题,因此两题均重定向至此页面。
AMC 10 试题
下图所示为直线 \( \ell \) ,其上具有正方形与线段构成的规则、无限、重复图案。

在此图形所在的平面内,以下四种刚体运动变换中,除恒等变换外,有多少种能将该图形变换为自身?
- 绕直线 \( \ell \) 上某点的某种旋转
- 关于直线 \( \ell \) 的反射
- 关于一条垂直于直线 \( \ell \) 的直线的某种反射
沿平行于直线 \( \ell \) 方向的某种平移
(A) 0 (B) 1 (C) 2 (D) 3 (E) 4
解答
陈述1为真。以朝上方块与朝下方块之间中点为中心旋转 \( {180}^{ \circ } \) ,所得图形与原图相同。
陈述2亦为真。向左或向右平移时,当上下图形重新对齐(图形在两端无限延伸),像将与自身重合。
陈述3为假。关于直线 \( \ell \) 的反射会将朝上方块变为朝下方块,反之亦然。
最后,陈述4亦为假,因为它会使从方块延伸出的对角线方向互换。因此,只有 \( c \) ,陈述为真。参见
2019 AMC 10A 试题/第9题
题目
最大的三位正整数 \( n \) 是多少,使得前 \( n \) 个正整数的和 \( \underline{not} \) 是前 \( n \) 个正整数的乘积的因数?
(A) 995 (B) 996 (C) 997 (D) 998 (E) 999
解法1
前 \( n \) 个正整数的和为 \( \frac{\left( n\right) \left( {n + 1}\right) }{2} \) ,我们希望它 \( n! \) (前 \( n \) 个正整数的乘积)的因数。注意,当且仅当 \( n + 1 \) 为合数时,其所有因数均小于或等于 \( n \) ,从而可与 \( n! \) 中的因数约去。因此,当 \( n + 1 \) 为合数时,前 \( n \) 个正整数的和是 \( n! \) 的因数。(注:此结论对所有正整数均成立,唯1除外,因为2不是1的因数/因子。)故在此情形下, \( n + 1 \) 必须为质数。最大的三位质数为997,因此减1得 \( n = 0 \) 。(B) 996。
解法2
与解法1相同,我们推断 \( n + 1 \) 必须为质数。若一时想不起最大的三位质数,可利用此结论排除选项中可能的 \( n \) 值。选项 \( A \) 、 \( C \) 和 \( E \) 不成立,因为 \( n + 1 \) 为偶数,而所有偶数均可被2整除,故选项 \( A \) 、 \( C \) 和 \( E \) 为合数而非质数。选项 \( D \) 亦不成立,因为999可被9整除,故为合数而非质数。因此,正确答案必为(B) 996
2019 AMC 10A 试题/第10题
题目
一块宽10英尺、长17英尺的矩形地面用170块边长为1英尺的正方形瓷砖铺满。一只虫子沿直线从一角爬到对角。包括起点和终点的瓷砖在内,虫子共经过多少块瓷砖?
(A) 17 (B) 25 (C) 26 (D) 27 (E) 28
解法1
虫子经过的瓷砖数等于1加上它穿越水平或垂直线的次数。它必须穿越16条水平线和9条垂直线,因此虫子总共经过 \( {16} + 9 + 1 = \) (C) 26块方格。
注:一般公式为 \( a + b - \gcd \left( {a, b}\right) \) ,因为需用穿越的垂直/水平线数减去穿越的角点数(避免重复计数)。本题中, \( {16} + 9 - 1 \) (因为 \( \gcd \left( {{16},9}\right) = 1 \) ),得24,但需再加2,因为起点和终点的瓷砖在一般公式中未被计入。
可通过斜率 \( \sim \) 看出为何是 \( \gcd \left( {a, b}\right) \) Williamgolly
解法2(作图法)
我们也可画出整个矩形地面的示意图或比例模型(可借助方格纸和/或直尺确保比例准确),然后直接数出路径穿过的瓷砖数。为简化操作,可将完整网格分成4个区域,只需画出其中一个5英尺×8.5英尺的区域。
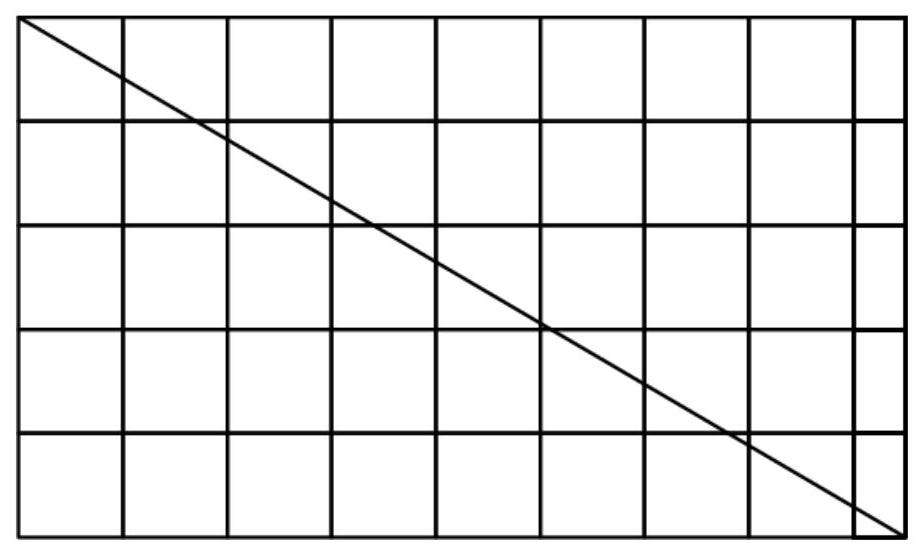
尽管画出的直线看似经过若干点,但由于10和17互质(即它们的最大公约数为1,又称gcd为1),直线实际上不会穿过任何格点,因此无论从哪一侧计数,穿过的方格数都相同。通过图示数出直线穿过的方格数为13,再乘以2,得到虫子在整个矩形地面上穿过的方格总数为 \( 2 \cdot {13} = \) (C) 26。
2019 AMC 10A 试题/第11题
题目
\( {201}^{9} \) 的正整数约数中,有多少个是完全平方数或完全立方数(或同时满足)? (A) 32 (B) 36 (C) 37 (D) 39 (E) 41
解法1
将 \( {201}^{9} \) 质因数分解,得到 \( {3}^{9} \cdot {67}^{9} \) 。完全平方数的所有质因数指数必须为偶数,因此3和67的指数可选0,2,4,6,8,共 \( 5 \cdot 5 = {25} \) 个完全平方数。
完全立方数(perfect cubes)的每个质因数的指数都必须是3的倍数,因此3和67的指数只能是0、3、6或9,这样共有 \( 4 \cdot 4 = {16} \) 个完全立方数,总计 \( {25} + {16} = {41} \) 。
减去重复计算的 \( 6\left( {{3}^{0} \cdot {67}^{0},{3}^{0} \cdot {67}^{6},{3}^{6} \cdot {67}^{0}}\right. \) 和 \( {3}^{6} \cdot {67}^{6} \) 的幂次后,我们得到 \( {41} - 4 = \) (C)37
解法2
注意到 \( {201} = {67} \cdot 3 \) 。现在分情况讨论:
情况1:因数为 \( {3}^{n} \) 。那么我们可以有 \( n = 2 \) 、3、4、6、8或9。
情况2:因数为 \( {67}^{n} \) 。这与情况1相同。
情况3:因数为3和67的某种组合。
如果允许任意组合,这会很简单,因为那样就会直接得到 \( 6 \cdot 6 \) 。然而,我们必须将生成平方数的数字与生成平方数的数字配对,立方数同理。简言之,让我们整理 \( n \) 的值。
\( n = 2 \) 是“平方数”(square),因为它会给出一个该数的因数是完全平方数(perfect square)。更一般地说,它是偶数。
\( n = 3 \) 是“立方数”(cube),因为它会给出一个该数的因数是完全立方数(perfect cube)。更一般地说,它是3的倍数。
\[ n = 4\text{is a "square".} \]
\( n = 6 \) 很有趣,因为它既是“平方数”又是“立方数”。不要将其计入任何一类,否则会造成重复计数,我们将在另一种情况中单独计算。
\[ n = 8\text{is a "square"} \]
\[ n = 9\text{is a "cube".} \]
现在考虑子情况:
子情况1:平方数彼此配对。
由于我们有3个平方项,它们会与另外3个平方项配对,因此有 \( 3 \cdot 3 = 9 \) 种可能。
子情况2:立方数彼此配对。
由于我们有2个立方项,它们会与另外2个立方项配对,因此有 \( 2 \cdot 2 = 4 \) 种可能。
子情况3:一个数字与 \( n = 6 \) 配对。
由于任何数字都可以与 \( n = 6 \) 配对(因为它既能得到平方又能得到立方),因此会有6种可能性。然而请记住,可能存在两个不同的底数(3和67),它们会产生不同的结果。因此,实际上共有 \( 6 \cdot 2 = {12} \) 种可能性。
最后,将所有情况相加得到 \( 6 + 6 + 9 + 4 + {12} = \) (C) 37
2019年AMC 10A试题/第12题
问题
梅拉妮计算了2019年各月份日期所构成的365个值的平均数 \( \mu \) 、中位数 \( M \) 以及众数。因此,她的数据包括 \( {12}1\mathrm{s} \) 、 \( {122}\mathrm{s} \) 、 \( \ldots \) 、 \( {1228}\mathrm{s} \) 、 \( {11}{29}\mathrm{s} \) 、 \( {1130}\mathrm{s} \) 和 \( {731}\mathrm{s} \) 。设 \( d \) 为众数的中位数。以下哪一项陈述为真?
(A) \( \mu < d < M \) (B) \( M < d < \mu \) (C) \( d = M = \mu \) (D) \( d < M < \mu \) (E) \( d < \mu \)
解决方案 1
首先, \( d \) 显然必须小于 \( M \) ,因为在计算 \( M \) 时,我们必须把29、30和31都考虑进去。因此可以排除选项 \( B \) 和 \( C \) 。由于总共有365条记录,中位数 \( M \) 必须是第 \( {183}\mathrm{{rd}} \) 个;此时我们注意到 \( {12} \cdot {15} \) 是180,所以16必定是中位数(因为183位于 \( {12} \cdot {15} + 1 = {181} \) 和 \( {12} \cdot {16} = {192} \) 之间)。现在,均值 \( \mu \) 必须小于16,因为29、30和31的数量要少得多。 \( d \) 又小于 \( \mu \) ,因为在计算 \( \mu \) 时会把29、30和31都计入。因此答案是 \( \mid \left( \mathbf{E}\right) d < \mu < M \)
解决方案 2
与解法1相同,我们求得中位数为16。接着观察众数(1–28),我们发现即使每种数字各出现12次,它们的中位数仍为14.5。至于平均数,前28个数的平均数恰好等于它们的中位数,即14.5。因此,由于实际存在29、30和31,平均数必然高于14.5。另一方面,29、30和31的数量少于其余数字,故平均数必然低于16(中位数)。比较这些数值,答案为 \( \mid \left( \mathbf{E}\right) d < \mu < M \)
解法3(直接计算)
我们只需仔细计算每个值即可解决此问题,结果分别为 \( M = {16} \) 、 \( d = {14.5} \) 和 \( \mu \approx {15.7} \) 。因此答案为 \( \left( \mathbf{E}\right) d < \mu < M \)
问题
设 \( \bigtriangleup {ABC} \) 为一等腰三角形,其中 \( {BC} = {AC} \) 与 \( \angle {ACB} = {40}^{ \circ } \) 。以 \( \overline{BC} \) 为直径作圆,并令 \( D \) 与 \( E \) 分别为圆与边 \( \overline{AC} \) 和 \( \overline{AB} \) 的其余交点。设 \( F \) 为四边形 \( {BCDE} \) 对角线的交点。求 \( \angle {BFC} \) 的度数。
(A) 90 (B) 100 (C) 105 (D) 110 (E) 120
解法1
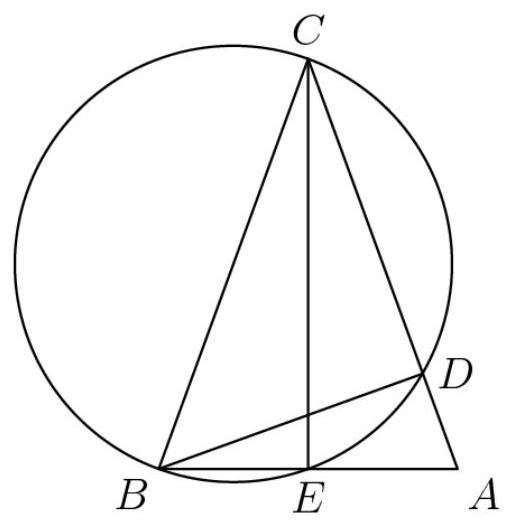
画出图形后,我们发现 \( \angle {BDC} \) 和 \( \angle {BEC} \) 是直角,因为它们内接于半圆。利用等腰三角形的性质,我们得到 \( \angle {ABC} = {70}^{ \circ } \) 。通过在 \( \bigtriangleup {ECB} \) 和 \( \bigtriangleup {DBC} \) 上应用三角形内角和,可以求出 \( \angle {ECB} = {20}^{ \circ } \) 和 \( \angle {DBC} = {50}^{ \circ } \) 。
\( {\angle BDC} + {\angle DCB} + {\angle DBC} = {180}^{ \circ }\;\Longrightarrow \;{90}^{ \circ } + {40}^{ \circ } + {\angle DBC} = {180}^{ \circ }\;\Longrightarrow \;{\angle DBC} = {50}^{ \circ } \)
\( {\angle BEC} + {\angle EBC} + {\angle ECB} = {180}^{ \circ }\;\Longrightarrow \;{90}^{ \circ } + {70}^{ \circ } + {\angle ECB} = {180}^{ \circ }\;\Longrightarrow \;{\angle ECB} = {20}^{ \circ } \)
接着,我们取三角形 \( {BFC} \) ,并求出 \( \angle {BFC} = {180}^{ \circ } - {50}^{ \circ } - {20}^{ \circ } = \) (D) \( {110}^{ \circ } \) 。
解法2
或者,我们也可以使用相似三角形。开头与解法1类似。
画出图形后,我们发现 \( \angle {BDC} \) 和 \( \angle {BEC} \) 是直角,因为它们内接于半圆。因此,
\[ \angle {BDA} = {180}^{ \circ } - \angle {BDC} = {180}^{ \circ } - {90}^{ \circ } = {90}^{ \circ }\text{.} \]
于是, \( \bigtriangleup {BEF} \sim {BDA} \) 由AA相似可得,因为 \( \angle {EBF} = \angle {DBA} \) 且 \( \angle {BEC} = {90}^{ \circ } = \angle {BDA} \) 。
因此,我们知道
\[ \angle {EFB} = \angle {DAB} = \angle {CAB} = {70}^{ \circ }\text{.} \]
最后,我们推得
\[ \angle {BFC} = {180}^{ \circ } - \angle {EFB} = {180}^{ \circ } - {70}^{ \circ } = ({D)}{110}^{ \circ }. \]
解法3(外角)
根据相交弦所成角的性质,我们得到
\[ m\angle {BFC} = \frac{m\overset{⏜}{\mathrm{{BC}}} + m\overset{⏜}{\mathrm{{DE}}}}{2} \]
根据外角定理,我们得到
\[ m\angle {CAB} = \frac{m\overset{⏜}{\mathrm{{BC}}} - m\overset{⏜}{\mathrm{{DE}}}}{2} \]
将两式相加,得到
\[ m\angle {BFC} - m\angle {CAB} = m\overset{⏜}{\mathrm{{BC}}} \Rightarrow m\angle {BFC} = m\overset{⏜}{\mathrm{{BC}}} - m\angle {CAB} \]
由于 \( \overset{⏜}{\mathrm{{BC}}} \) 是直径, \( m\overset{⏜}{\mathrm{{BC}}} = {180}^{ \circ } \) ,且 \( \bigtriangleup {ABC} \) 为等腰三角形且 \( m\angle {ACB} = {40}^{ \circ } \) ,因此 \( m\angle {CAB} = {70}^{ \circ } \) 。于是
\[ m\angle {BFC} = {180}^{ \circ } - {70}^{ \circ } = \text{ (D) }{110}^{ \circ } \]
解法4
注意到若 \( \angle {BEC} = {90}^{ \circ } \) ,则 \( \angle {BCE} \) 与 \( \angle {ACE} \) 必为 \( {20}^{ \circ } \) 。利用圆内接四边形性质(或同弧所对圆周角性质),可得 \( \angle {EBD} \cong \angle {ECD} = {20}^{ \circ } \) 。于是
\( \angle {CBF} = {70} - {20} = {50}^{ \circ } \) ,因此 \( \angle {BFC} = {180} - {20} - {50} = {110}^{ \circ } \) ,即 \( \mathbf{\left\lbrack O\right\rbrack } \)
解法5(作弊法)
若看不出解法,可直接画精确图并用量角器测得该角为110-(D)。参见
2019 AMC 10A 第14题
以下题目同时出现在2019 AMC 10A第14题与2019 AMC 12A第8题,故两题均重定向至此页。
题目
平面上四条互异直线,恰有 \( N \) 个不同的点位于两条或更多直线上。求 \( N \) 所有可能取值之和。
(A) 14 (B) 16 (C) 18 (D) 19 (E) 21
解答
如下图所示,可得到0、1、3、4、5、6个交点:
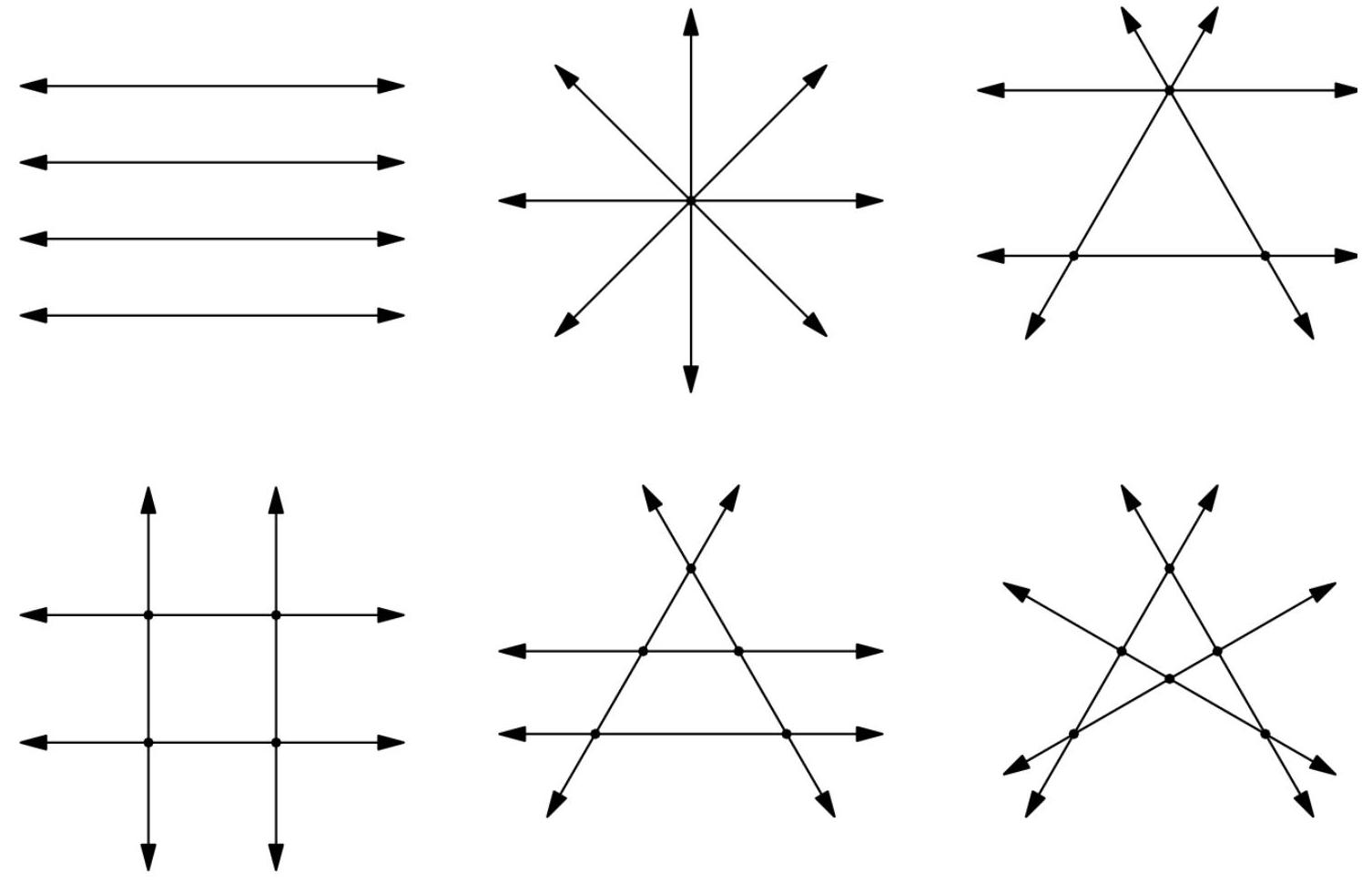
显然,最大可能交点数为 \( \left( \begin{matrix} 4 \\ 2 \end{matrix}\right) = 6 \) ,因每两条直线至多交于一点。现证无法得到两个交点。
用反证法。假设存在四条直线恰有两个交点,设其为 \( A \) 与 \( B \) 。分两种情况:
情况1:无直线同时经过 \( A \) 与 \( B \)
于是,因交点至少由两直线相交而成, \( A \) 与 \( B \) 处各有两直线通过。又因无更多交点,过 \( A \) 的任一直线必与过 \( B \) 的任一直线平行,故过 \( A \) 的直线与过 \( B \) 的直线分别平行。由平行传递性,过 \( B \) 的两直线互相平行,从而重合,矛盾。
情况2:存在一条直线同时经过 \( A \) 与 \( B \)
那么必有一条直线 \( {l}_{a} \) 经过 \( A \) ,一条直线 \( {l}_{b} \) 经过 \( B \) 。这两条直线必须平行。第四条直线 \( l \) 必须经过 \( A \) 或 \( B \) 。不失一般性,设 \( l \) 经过 \( A \) 。由于 \( l \) 与 \( {l}_{a} \) 不能重合,它们不能平行;于是 \( l \) 与 \( {l}_{b} \) 也不能平行,从而二者相交,产生矛盾。
所有可能性均已穷尽,因此我们可以断定两个交点是不可能的。我们的答案由和给出 \( 0 + 1 + 3 + 4 + 5 + 6 = \) (D) 19
2019 AMC 10A 问题/第15题
问题
一个数列由 \( {a}_{1} = 1,{a}_{2} = \frac{3}{7} \) 递归定义,且
\[ {a}_{n} = \frac{{a}_{n - 2} \cdot {a}_{n - 1}}{2{a}_{n - 2} - {a}_{n - 1}} \]
对所有 \( n \geq 3 \) ,则 \( {a}_{2019} \) 可写成 \( \frac{p}{q} \) ,其中 \( p \) 与 \( q \) 为互质的正整数。 \( p + q \) 是多少?
(A) 2020 (B) 4039 (C) 6057 (D) 6061 (E) 8078
解法1(归纳法)
利用递推公式,我们得到 \( {a}_{3} = \frac{3}{11} \) 、 \( {a}_{4} = \frac{3}{15} \) ,依此类推。似乎对所有 \( n \) 都有 \( {a}_{n} = \frac{3}{{4n} - 1} \) 。令 \( n = {2019} \) ,我们得到 \( {a}_{2019} = \frac{3}{8075} \) ,因此答案为 \( \sigma \) 到8078。为证明此公式,我们使用归纳法。已知 \( {a}_{1} = 1 \) 与 \( {a}_{2} = \frac{3}{7} \) ,满足我们的公式。现假设该公式对所有 \( n \leq m \) (某正整数 \( m \) )成立。根据假设, \( {a}_{m - 1} = \frac{3}{{4m} - 5} \) 与 \( {a}_{m} = \frac{3}{{4m} - 1} \) 。利用递推公式,
\[ {a}_{m + 1} = \frac{{a}_{m - 1} \cdot {a}_{m}}{2{a}_{m - 1} - {a}_{m}} = \frac{\frac{3}{{4m} - 5} \cdot \frac{3}{{4m} - 1}}{2 \cdot \frac{3}{{4m} - 5} - \frac{3}{{4m} - 1}} = \frac{\left( {\frac{3}{{4m} - 5} \cdot \frac{3}{{4m} - 1}}\right) \left( {{4m} - 5}\right) \left( {{4m} - 1}\right) }{\left( {2 \cdot \frac{3}{{4m} - 5} - \frac{3}{{4m} - 1}}\right) \left( {{4m} - 5}\right) \left( {{4m} - 1}\right) } = \frac{1}{6({4m} - } \]
故归纳完成。
解法2
由于我们关心的是分子与分母之和,考虑由 \( {b}_{n} = \frac{1}{{a}_{n}} \) 定义的数列。
\( {b}_{n} = 2{b}_{n - 1} - {b}_{n - 2} = 3{b}_{n - 2} - 2{b}_{n - 3} = 4{b}_{n - 3} - 3{b}_{n - 4} = \ldots \)
依此模式递归,可见 \( {b}_{n} = \left( {n - 1}\right) \cdot {b}_{2} - \left( {n - 2}\right) \cdot {b}_{1} \) 。
代入2019,我们得到 \( {b}_{2019} = {2018} \cdot \frac{7}{3} - {2017} = \frac{8075}{3} \) 。因分子与分母互质,答案为(E) 8078 -eric2020
解法3
将方程转化为其他形式似乎合理。令 \( {a}_{n} = x \) 、 \( {a}_{n - 1} = y \) 、 \( {a}_{n - 2} = z \) 。于是我们有
\[ x = \frac{zy}{{2z} - y} \]
\[ {2xz} - {xy} = {zy} \]
\[ {2xz} = y\left( {x + z}\right) \]
\[ y = \frac{2xz}{x + z} \]
因此, \( y \) 是 \( x \) 与 \( z \) 的调和平均数(harmonic mean)。这意味着 \( {a}_{n} \) 为调和数列,或等价地 \( {b}_{n} = \frac{1}{{a}_{n}} \) 为等差数列。现在我们有 \( {b}_{1} = 1 \) 、 \( {b}_{2} = \frac{7}{3} \) 、 \( {b}_{3} = \frac{11}{3} \) ,依此类推。由于公差为 \( \frac{4}{3} \) ,可将 \( {b}_{n} \) 显式表示为 \( {b}_{n} = \frac{4}{3}\left( {n - 1}\right) + 1 \) 。于是 \( {b}_{2019} = \frac{4}{3}\left( {{2019} - 1}\right) + 1 = \frac{8075}{3} \) ,从而 \( {a}_{2019} = \frac{3}{8075} = \frac{p}{q} \) 。 \( p + q = 0 \) (E) \( {8078} \sim \) jakeg314
2019 AMC 10A 试题/第16题
以下题目同时出现在2019 AMC 10A第16题和2019 AMC 12A第10题,因此两道题均重定向至此页面。
题目
下图所示为13个半径为1的圆位于一个更大的圆内。所有交点均发生在切点处。求图中阴影区域——即位于大圆内但在所有半径为1的圆之外的区域——的面积。
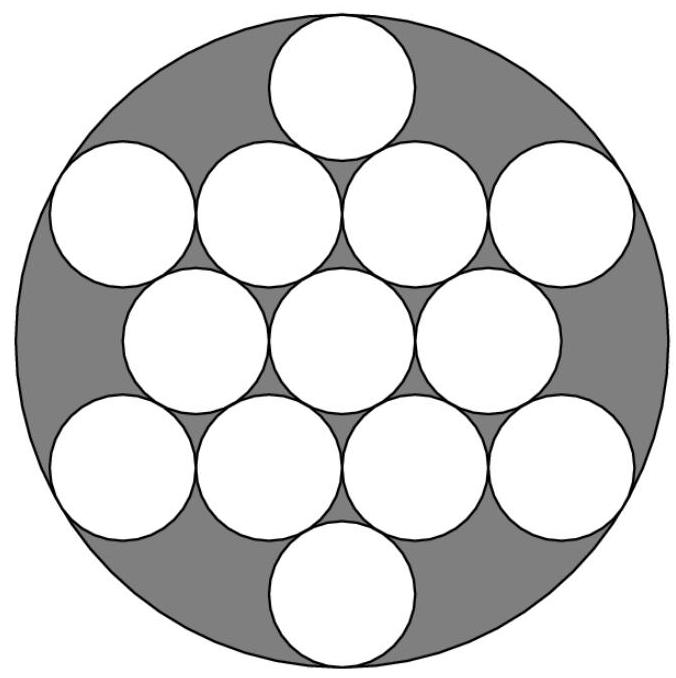
(A) \( {4\pi }\sqrt{3} \) (B) \( {7\pi } \) (C) \( \pi \left( {3\sqrt{3} + 2}\right) \) (D) \( {10\pi }\left( {\sqrt{3} - 1}\right) \) (E) \( \pi \left( {\sqrt{3} + 6}\right) \)
解法1
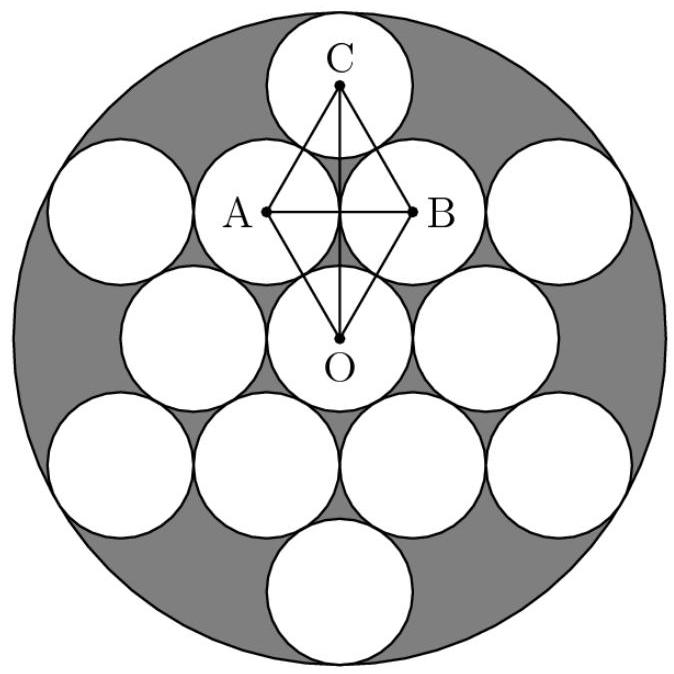
在上图中,注意到三角形 \( {OAB} \) 与三角形 \( {ABC} \) 全等且为边长为2的等边三角形。可以看出,大圆的半径等于三角形 \( O{AB} \) 的高度的两倍再加1(点 \( C \) 到圆边的距离)。利用 \( {30}^{ \circ } - {60}^{ \circ } - {90}^{ \circ } \) 三角形,可知该高为 \( \sqrt{3} \) 。因此,大圆的半径为 \( 2\sqrt{3} + 1 \) 。
于是大圆的面积为 \( {\left( 2\sqrt{3} + 1\right) }^{2}\pi = \left( {{13} + 4\sqrt{3}}\right) \pi \) ,而所有小圆面积之和为 \( {13\pi } \) ,故阴影区域面积为 \( \left( {{13} + 4\sqrt{3}}\right) \pi - {13\pi } = \) (A) \( {4\pi }\sqrt{3} \)
解法2
我们可以用三个与外层圆相切的单位圆的圆心构成一个边长为6的等边三角形。外层圆的半径等于该三角形的外接圆半径加1。利用 \( R = \frac{abc}{4A} \) 或 \( R = \frac{a}{2\sin A} \) ,可得半径为 \( \frac{6}{\sqrt{3}} + 1 \) 。
因此阴影面积为 \( \pi \left( {{\left( \frac{6}{\sqrt{3}} + 1\right) }^{2} - {13}}\right) = \sigma \left\lbrack {\sigma {\left( A\right) }^{ - }{4\pi }\sqrt{3}}\right\rbrack \)
解法3
与解法2类似,我们可用三个与外层圆相切的单位圆的圆心构成边长为6的等边三角形。可求得该三角形的高为 \( 3\sqrt{3} \) 。接着,可用第三行第二个、第三个圆以及最底端圆的圆心构成边长为2的等边三角形,其高显然为 \( \sqrt{3} \) 。因此大圆的直径为 \( 4\sqrt{3} + 2 \) ,半径为
\( \frac{4\sqrt{3} + 2}{2} = 2\sqrt{3} + 1 \) 。于是大圆的面积为
\( \pi {\left( 2\sqrt{3} + 1\right) }^{2} = \pi \cdot \left( {{13} + 4\sqrt{3}}\right) = {13\pi } + {4\pi }\sqrt{3} \) 。13个小圆的总面积为 \( {13\pi } \) ,故
阴影面积为 \( \left( {{13\pi } + {4\pi }\sqrt{3}}\right) - {13\pi } = \left( \mathbf{A}\right) {4\pi }\sqrt{3} \) 。
解法4
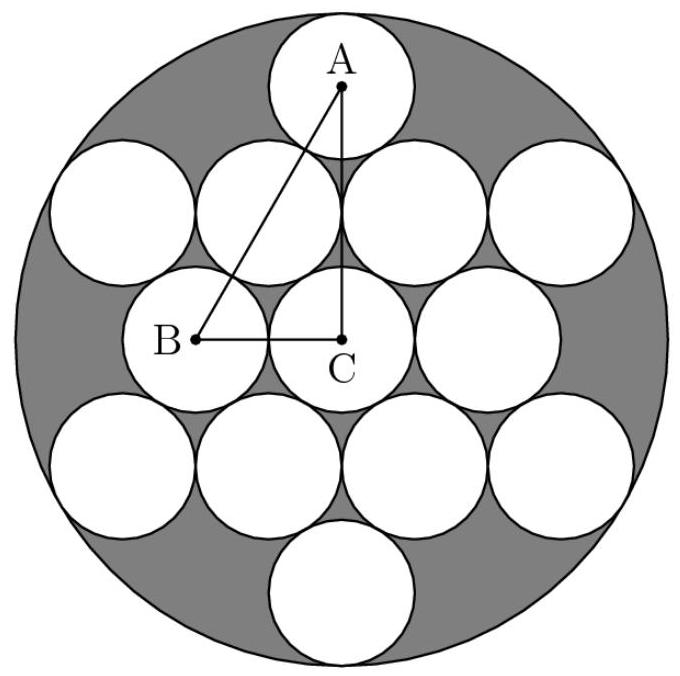
在上图中, \( {AB} = 4 \) 且 \( {BC} = 2 \) ,因此 \( {AC} = \sqrt{{4}^{2} - {2}^{2}} = 2\sqrt{3} \) 。大圆的半径为 \( {AC} + 1 = 2\sqrt{3} + 1 \) ,故大圆的面积为 \( \pi {\left( 2\sqrt{3} + 1\right) }^{2} = \pi \left( {{13} + 4\sqrt{3}}\right) = {13\pi } + {4\pi }\sqrt{3} \) 。现在,减去两个小圆的总面积,得到 \( {13\pi } + {4\pi }\sqrt{3} - {13\pi } = 0 \) (A) \( {4\pi }\sqrt{3} \) 。
2019 AMC 10A 试题/第17题
题目
一个孩子用形状相同但颜色不同的小立方体搭塔。若他有2个红色立方体、3个蓝色立方体和4个绿色立方体,可搭出多少种高为8个立方体的不同塔?(会剩下1个立方体。)
(A) 24 (B) 288 (C) 312 (D) 1,260 (E) 40,320
解法1
排列8个立方体等价于先排列9个立方体,再把最后一个拿掉。换句话说,每一种9个立方体的排列与每一种实际有效的8个立方体排列一一对应。因此,我们最初得到 \( 9! \) 。然而,我们重复计数了,因为红色立方体可以互换而不改变整体排列,蓝色和绿色立方体同理。因此,需要除以红色立方体的 \( 2! \) 种排列方式、蓝色立方体的 \( 3! \) 种排列方式以及绿色立方体的 \( 4! \) 种排列方式。于是我们有
\( \frac{9!}{2! \cdot 3! \cdot 4!} = \) (D) 1,260 种不同的塔。
注:可更简洁地写作
\[ \left( \begin{matrix} 9 \\ 2,3,4 \end{matrix}\right) = \left( \begin{array}{l} 9 \\ 2 \end{array}\right) \left( \begin{matrix} 9 - 2 \\ 3 \end{matrix}\right) \left( \begin{matrix} 9 - \left( {2 + 3}\right) \\ 4 \end{matrix}\right) = 1,{260} \]
解法2
我们可以把问题分成三种情况,每种情况对应排除一个立方体:情况1:排除红色立方体。此时需排列1个红色立方体、3个蓝色立方体和4个绿色立方体。可能的排列数为 \( \frac{8!}{4! \cdot 3!} = {280} \) 。注意,我们无需乘以红色立方体的数量,因为两个红色立方体无法区分。
情况2:排除蓝色立方体。此时需排列2个红色立方体、2个蓝色立方体和4个绿色立方体。可能的排列数为
\[ \frac{8!}{2! \cdot 2! \cdot 4!} = {420} \]
情况3:排除绿色立方体。此时需排列2个红色立方体、3个蓝色立方体和3个绿色立方体。可能的排列数为
\[ \text{is}\frac{8!}{2! \cdot 3! \cdot 3!} = {560}\text{.} \]
将以上各情况的数目相加,得到答案为
\[ {280} + {420} + {560} = \left( \mathbf{D}\right) 1,{260}. \]
解法3(猜测)
如果时间不够,请注意选项 \( A \) 、 \( B \) 和 \( C \) 都太小,而选项 \( E \) 毫无意义,因为它将直接等于 \( 8! \) ,仿佛没有任何限制。因此,通过有根据的猜测和排除法,正确答案必定是(D) 1,260
注意:不推荐使用此策略!
另见
| 2019年AMC 10A(题目 \( \cdot \) 答案 \( \cdot \) 资源(http://www.artofproblemsolving.com/Forum/resources.php?c=182&cid=43&year=2019)) | |
| 上一题:第16题 | 下一题:第18题 |
| \( 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7 \cdot 8 \cdot 9 \cdot {10} \cdot {11} \cdot {12} \cdot {13} \cdot {14} \cdot {15} \cdot {16} \cdot {17} \cdot {18} \) - 19・20・21・22・23・24・25 | |
| 所有AMC 10题目与解答 | |
2019 AMC 10A 试题/第18题
题目
对于某个正整数 \( k \) ,(十进制)分数 \( \frac{7}{51} \) 在 \( k \) 进制下的循环小数表示为 \( 0.{\overline{23}}_{k} = {0.232323}\ldots \) k。 \( k \) 是多少?
(A) 13 (B) 14 (C) 15 (D) 16 (E) 17
解法1
我们可以将分数 \( 0.{\overline{23}}_{k} \) 展开如下:
\( 0.{\overline{23}}_{k} = 2 \cdot {k}^{-1} + 3 \cdot {k}^{-2} + 2 \cdot {k}^{-3} + 3 \cdot {k}^{-4} + \ldots \) 注意到这等价于
\[ 2\left( {{k}^{-1} + {k}^{-3} + {k}^{-5} + \ldots }\right) + 3\left( {{k}^{-2} + {k}^{-4} + {k}^{-6} + \ldots }\right) \]
通过求几何级数和并化简,我们得到 \( \frac{{2k} + 3}{{k}^{2} - 1} = \frac{7}{51} \) 。解这个二次方程(或直接检验选项)可得答案 \( k = \left| {\left( \mathbf{D}\right) {16}}\right| \)
解法2
设 \( a = {0.2323}\ldots \) , \( k \) 。因此, \( {k}^{2}a = {23.2323}\ldots \) ,
由此我们得到 \( {k}^{2}a - a = {23}_{k} \) ,所以 \( a = \frac{{23}_{k}}{{k}^{2} - 1} = \frac{{2k} + 3}{{k}^{2} - 1} = \frac{7}{51} \) 。
现在,与解法1类似,我们可以检验 \( {2k} + 3 \) 是否为7的倍数,或真正解二次方程,从而得到答案(D,16)。
解法3(暴力枚举)
我们只需将所有选项作为 \( k \) 的值代入,看看哪一个成立。经过传奇般、惊人、历史性的伟大计算,最终得到(D) 16为答案。
解法4
与解法1一样,我们得到方程 \( \frac{{2k} + 3}{{k}^{2} - 1} = \frac{7}{51} \) 。
我们现在可以将其改写为 \( \frac{{2k} + 3}{\left( {k - 1}\right) \left( {k + 1}\right) } = \frac{7}{51} = \frac{7}{3 \cdot {17}} \) 。注意到
\( {2k} + 3 = 2\left( {k + 1}\right) + 1 = 2\left( {k - 1}\right) + 5 \) 。由于17是素数,因此 \( k - 1 \) 和 \( k + 1 \) 中必有一个能被17整除。现在逐一检查各选项,可得(D) 16。
解法5
假设你已熟悉基本循环小数的规则, \( {0.232323}\ldots = \frac{23}{99} \) 。现在我们希望基数 \( k \) 满足 \( {23} = 7\left( {{mod}\;k}\right) \) 和 \( {99} = {51}\left( {{mod}\;k}\right) \) ,原因是我们想把该数从十进制转换为 \( k \) 进制。由第一个方程可知, \( k \) 必须等于9、16、23,或一般地等于 \( {7n} + 2 \) 。该集合中唯一出现在选项中的数是16。将其代入第二个方程 \( {99} = {51}\left( {\;\operatorname{mod}\;k}\right) \) 验证,等式成立。因此答案为(D) 16。
2019 AMC 10A 试题/第19题
题目
的最小可能值是多少
\[ \left( {x + 1}\right) \left( {x + 2}\right) \left( {x + 3}\right) \left( {x + 4}\right) + {2019} \]
其中 \( x \) 为实数?
(A) 2017 (B) 2018 (C) 2019 (D) 2020 (E) 2021
解法1
将首尾两项与中间两项分别组合,得 \( \left( {{x}^{2} + {5x} + 4}\right) \left( {{x}^{2} + {5x} + 6}\right) + {2019} \) ,可化简为 \( {\left( {x}^{2} + 5x + 5\right) }^{2} - 1 + {2019} \) 。注意到平方非负,且存在实数 \( x \) 使 \( {x}^{2} + {5x} + 5 = 0 \) 成立,故答案为 \( \left| {\text{ }\text{B }\text{ 2018 }}\right| \) 。Williamgolly的更易理解解法:因式分解为 \( \left( {{x}^{2} + {5x} + 4}\right) \left( {{x}^{2} + {5x} + 6}\right) + {2019} \) 后,令 \( y = {x}^{2} + {5x} + 5 \) ,则原式变为 \( \left( {y - 1}\right) \left( {y + 1}\right) + {2019} = {y}^{2} + {2018} \) 。显然 \( {y}^{2} \) 非负,故当 \( y = 0 \) 时取最小值,此时表达式等于2018。解法2 设 \( a = x + \frac{5}{2} \) ,则表达式 \( \left( {x + 1}\right) \left( {x + 2}\right) \left( {x + 3}\right) \left( {x + 4}\right) \) 变为 \( \left( {a - \frac{3}{2}}\right) \left( {a - \frac{1}{2}}\right) \left( {a + \frac{1}{2}}\right) \left( {a + \frac{3}{2}}\right) \) 。
我们可用平方差公式得到 \( \left( {{a}^{2} - \frac{9}{4}}\right) \left( {{a}^{2} - \frac{1}{4}}\right) \) ,再展开得 \( {a}^{4} - \frac{5}{2}{a}^{2} + \frac{9}{16} \) 。
通过配方法重构此式,得到 \( {\left( {a}^{2} - \frac{5}{4}\right) }^{2} - 1 \) ,其最小值为-1。因此答案为 \( {2019} - 1 = \) (B) 2018
解法3(微积分)
与解法1类似,将首末项与中项分别组合,得到 \( \left( {{x}^{2} + {5x} + 4}\right) \left( {{x}^{2} + {5x} + 6}\right) + {2019} \)
令 \( y = {x}^{2} + {5x} \) ,得到表达式 \( \left( {y + 4}\right) \left( {y + 6}\right) + {2019} \) 。现在,我们求 \( \left( {y + 4}\right) \left( {y + 6}\right) \) 的临界点以使函数最小化:
\[ \frac{d}{dx}\left( {{y}^{2} + {10y} + {24}}\right) = 0 \]
\[ {2y} + {10} = 0 \]
\[ {2y}\left( {y + 5}\right) = 0 \]
\[ y = - 5,0 \]
为使结果最小,我们使用 \( y = - 5 \) 。因此最小值为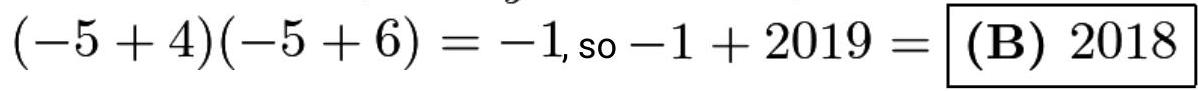
注:我们亦可利用抛物线最小/最大值点
\( y = a{x}^{2} + {bx} + c \) 出现在 \( x = - \frac{b}{2a} \) 。
解法4
当奇数个因子为负时,该表达式为负。这种情况
发生在 \( - 2 < x < - 1 \) 或 \( - 4 < x < - 3 \) 。代入 \( x = - \frac{3}{2} \) 或 \( x = - \frac{7}{2} \)
得到 \( - \frac{15}{16} \) ,非常接近-1。因此答案为
\( - 1 + {2019} = \left( \begin{array}{l} \mathbf{B} \end{array}\right) {2018} \)
解法5(利用选项)
选项 \( C, D \) 和 \( E \) 不可能,因为
\( \left( {x + 1}\right) \left( {x + 2}\right) \left( {x + 3}\right) \left( {x + 4}\right) \) 可能为负(例如当 \( x = - \frac{3}{2} \) 时可见)
)。代入 \( x = - \frac{3}{2} \) 可见其变为 \( {2019} - \frac{15}{16} \) ,故四舍五入为
(B) 2018
我们还可看出函数极限至少为-1,因为在最小值处,有两个数小于1,而另两个介于1与2之间。
2019 AMC 10A 试题/第20题
问题
将数字 \( 1,2,\ldots ,9 \) 随机填入 \( 3 \times 3 \) 网格的9个方格中。每个方格填入一个数字,每个数字恰好使用一次。求每一行与每一列的数字之和均为奇数的概率。
(A) \( \frac{1}{21} \) (B) \( \frac{1}{14} \) (C) \( \frac{5}{63} \) (D) \( \frac{2}{21} \) (E) \( \frac{1}{7} \)
解决方案 1
注意,奇数和只能由(e, e, o)或 \( \left( {o, o, o}\right) , \) 构成,因此我们专注于放置偶数:需要让每一行/列中的每个偶数都与另一个偶数配对。可以看出,共有9种方法。然后有 \( 5! \) 种方式排列奇数, \( 4! \) 种方式排列偶数,从而得到
答案为 \( \frac{5! \cdot 4! \cdot 9}{9!} = 6 \) (B) \( \frac{1}{14} \) 。
解决方案 2
根据鸽巢原理(Pigeonhole Principle),必然存在至少一行含有2个或更多奇数。因此,该行必须包含3个奇数,才能使行和为奇数。对列也可作同样论证。于是,我们只需选定一行和一列,将其全部填为奇数,这样得到的奇偶配置总数(不考虑具体是哪些奇数或偶数)即为所求。
放置的位置) 是 \( 3 \cdot 3 = 9 \) 。分母将是 \( \left( \begin{array}{l} 9 \\ 4 \end{array}\right) \) ,即所有可能方式的总数
我们可以选择9个方格中的哪4个将包含一个偶数。因此答案是
\[ \frac{9}{\left( \begin{array}{l} 9 \\ 4 \end{array}\right) } = \text{ (B) }\frac{1}{14} \]
2019年AMC 10A试题/第21题
问题
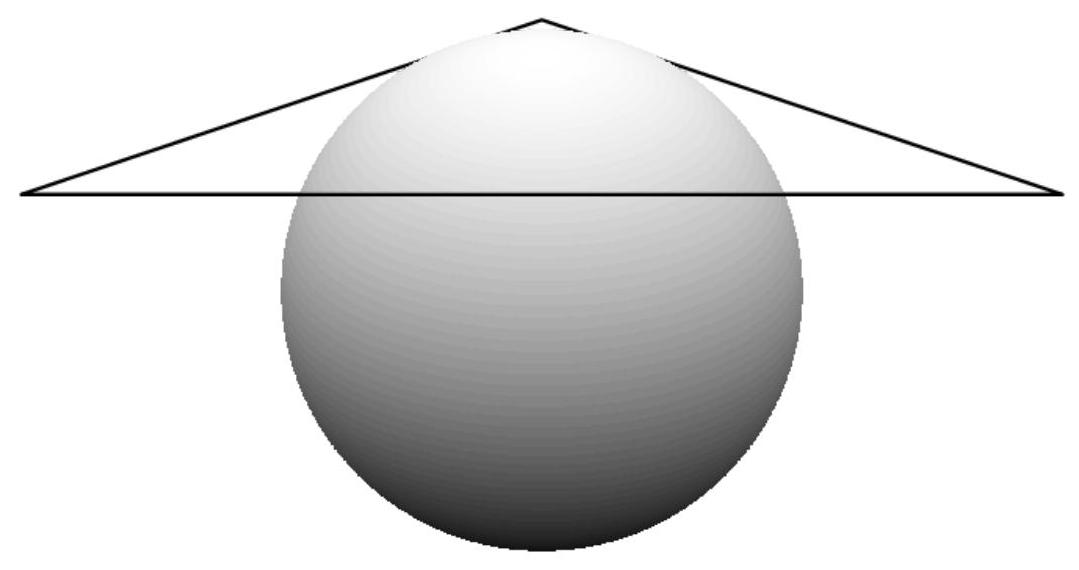
一个以 \( O \) 为球心的球,半径为6。空间中有一个边长为15、15、24的三角形,其每条边都与该球相切。求 \( O \) 到该三角形所在平面的距离。
(A) \( 2\sqrt{3} \) (B) 4 (C) \( 3\sqrt{2} \) (D) \( 2\sqrt{5} \) (E) 5 示意图
3D:
穿过三角形的平面:
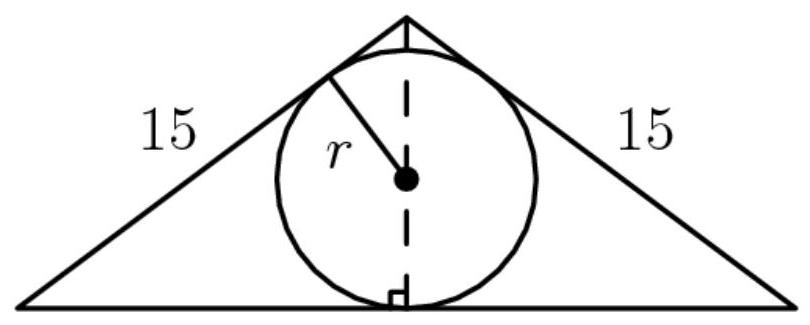
24
解法1
将三角形放置在球面上,使其三条边均与球相切。由三角形所在平面截球所得截面即为该三角形的内切圆。为求内切圆半径,使用面积 \( = \mathrm{{inradius}} \cdot \mathrm{{semiperimeter}} \) 。三角形面积可通过从长度为15的两边夹角顶点向长度为24的边中点作高求得。利用勾股数9-12-15,可迅速确定底边为24,高为9。公式
\ $ \\frac \{\\text{底} \\cdot \\text{高}\} \{2\}\ $
得三角形面积为108,半周长则为
\( \frac{{15} + {15} + {24}}{2} = {27} \) 。代入方程后,我们得到
\( {108} = \mathrm{{inradius}} \cdot {27} \) ,故内切圆半径为4。现设 \( O \) 与三角形之间的距离为 \( x \) 。在内切圆上任取一点,记为 \( A \) 。距离 \( {OA} \) 为6,因其恰为球半径。点 \( A \) 到内切圆中心的距离为4,因该距离即内切圆半径。利用勾股
定理,我们求得 \( x = \sqrt{{6}^{2} - {4}^{2}} = \sqrt{20} = \left| {\text{(D) }2\sqrt{5}}\right| \) 。
解法2(不利用内切圆半径)
在等腰三角形中作高。设所得3-4-5直角三角形 \( {ABC} \) 的 \( {AB} = {15} \) 与 \( {BC} = {12} \) 。根据特殊三角形性质, \( {AC} = 9 \) 。设圆半径为 \( r \) ,圆心为 \( O \) , \( D \) 为 \( {AB} \) 上距 \( O \) 最近的点。
则 \( {OD} = r \) 。显然, \( {ODBC} \) 为筝形。因此 \( {BC} = {DB} = {12} \) ,且 \( {AD} = {15} - {DB} = 3 \) 。 \( {AO} = {AC} - r = 9 - r \) 。由勾股定理, \( A{D}^{2} + O{D}^{2} = A{O}^{2} \) ,故 \( {3}^{2} + {r}^{2} = {\left( 9 - r\right) }^{2} \) 。 \( {r}^{2} \) 项相消,得 \( r = 4 \) 。
如前所述,再次运用勾股定理,距离为 \( \sqrt{{6}^{2} - {4}^{2}} = \left| {\mathbf{\left( D\right) }2\sqrt{5}}\right| \)
(解法由BJHHar提供)
解法3
与解法1相同,由勾股定理可知三角形高为9,且三角形三边均与球相切,故球截面中的圆即为三角形的内切圆。
回忆内切圆半径为角平分线交点。为求内切圆半径,我们使用角平分线定理。
\[ \frac{AB}{BI} = \frac{AD}{DI} \]
\[ \Rightarrow \frac{15}{BI} = \frac{12}{DI} \]
\[ \Rightarrow \frac{BI}{5} = \frac{DI}{4} \]
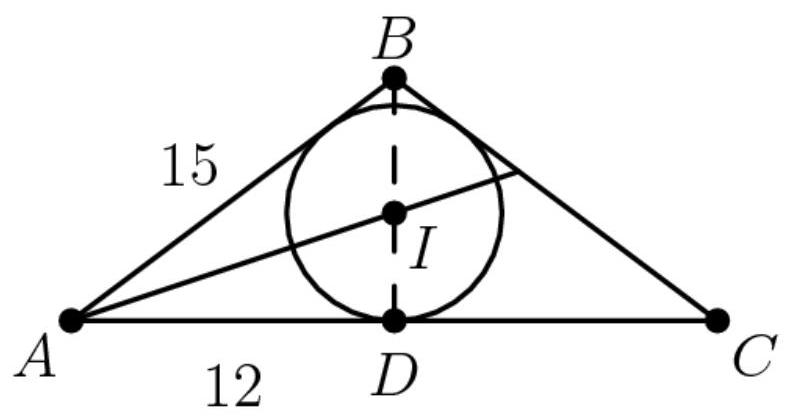
已知 \( {BI} + {DI} \) (高)等于9, \( {DI} \) (内切圆半径)为4。此后,可按解法1相同步骤求解。答案为(D) \( 2\sqrt{5} \) 。
解法4(相似三角形)
首先,我们标记几个点:
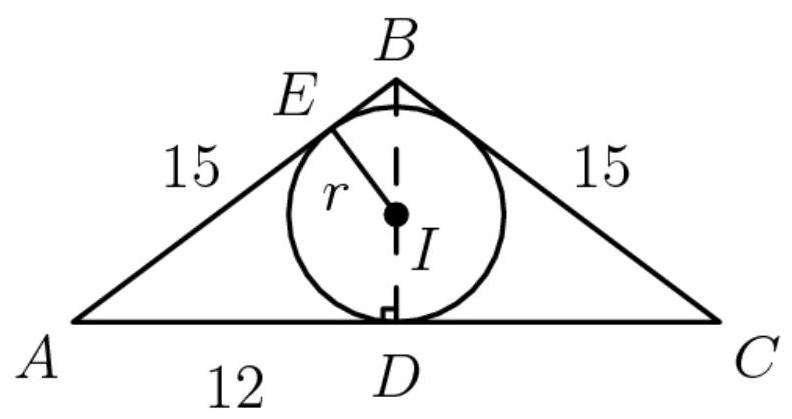
我们有 \( \bigtriangleup {BDC} \) 是一个 \( 3 - 4 - 5 \) 三角形,因此,如解法1所示, \( {BD} = 9 \) 。由此可知 \( \overline{BI} = 9 - r \) 。由于 \( {AB} \) 与圆 \( I \) 相切,我们还知道 \( I{EB} \) 是一个直角三角形。 \( \bigtriangleup {BIE} \) 和 \( \bigtriangleup {BDA} \) 共享角 \( {DBA} \) ,因此 \( \bigtriangleup {BIE} \sim \bigtriangleup {BDA} \) 因为它们有两个相等的角。因此,根据这种相似性, \( \frac{9 - r}{5} = \frac{r}{4} \) 。交叉相乘,我们得到 \( {36} - {4r} = {5r} \) ,从而得到 \( r = 4 \) 。现在我们取球体的另一个横截面,垂直于三角形的平面。
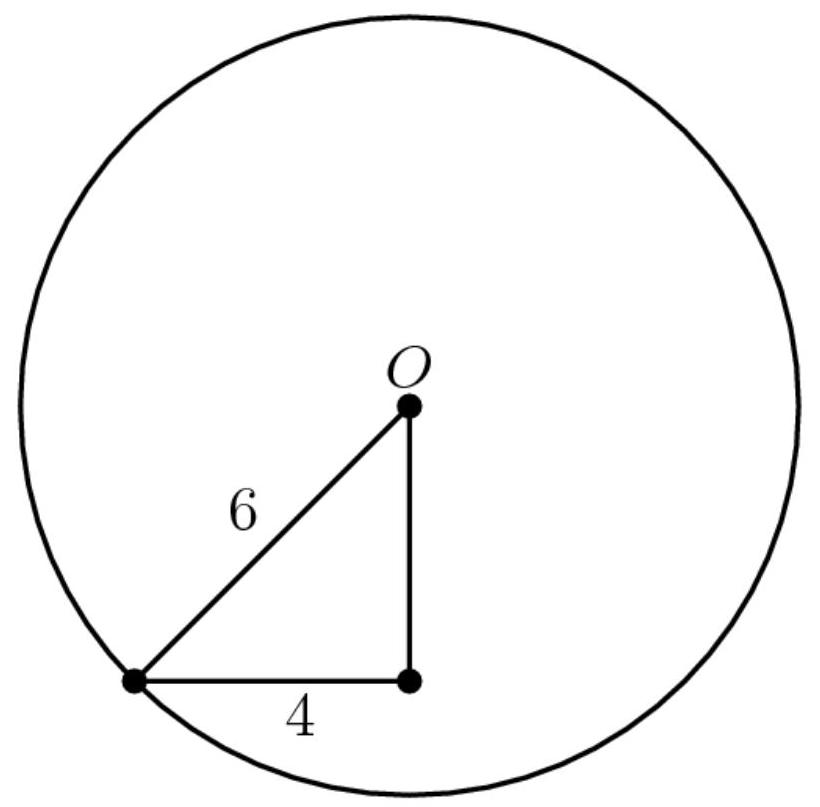
使用勾股定理,我们求出球心到平面的距离(D) \( 2\sqrt{5} \) 。
解法由woofle628和GeniusKid1221提供
2019 AMC 10A 试题/第22题
以下问题同时出现在2019 AMC 10A第22题和2019 AMC 12A第20题,因此两个问题都重定向到此页面。
问题
在0到1之间(含端点)的实数按以下方式选择。抛一枚公平硬币。如果正面朝上,则再抛一次,若第二次为正面则选数为0,若为反面则选数为1。另一方面,如果第一次抛硬币为反面,则从闭区间 \( \left\lbrack {0,1}\right\rbrack \) 中均匀随机选择一个数。两个随机数 \( x \) 和 \( y \) 以这种方式独立选择。 \( \left| {x - y}\right| > \frac{1}{2} \) 的概率是多少?
(A) \( \frac{1}{3} \) (B) \( \frac{7}{16} \) (C) \( \frac{1}{2} \) (D) \( \frac{9}{16} \) (E) \( \frac{2}{3} \)
解法
根据确定 \( x \) 时的第一次抛硬币结果和确定 \( y \) 时的第一次抛硬币结果,有几种情况。
四种情况如下:
情况1: \( x \) 为0或1,且 \( y \) 为0或1。
情况2: \( x \) 为0或1,且 \( y \) 从区间 \( \left\lbrack {0,1}\right\rbrack \) 中选择。
情况3: \( x \) 从区间 \( \left\lbrack {0,1}\right\rbrack \) 中选择,且 \( y \) 为0或1。
情况4: \( x \) 从区间 \( \left\lbrack {0,1}\right\rbrack \) 中选取, \( y \) 也从区间 \( \left\lbrack {0,1}\right\rbrack \) 中选取。
每种情况发生的概率为 \( \frac{1}{4} \) (因为需要两次抛硬币)。
对于情况1,我们需要 \( x \) 和 \( y \) 不同。因此,情况1的成功概率为。
在区间 \( \left\lbrack {0,\frac{1}{2}}\right) \) 内。无论 \( x \) 是什么,情况2的成功概率为
根据对称性,情况3与情况2具有相同的成功率。
对于案例4,我们必须使用几何概率(geometric probability),因为无论是否满足不等式,都存在无限多对可选组合。绘制 \( \left| {x - y}\right| > \frac{1}{2} \) 后,我们得到下图,其中阴影区域表示满足该不等式的所有点的集合:

阴影区域为 \( \frac{1}{4} \) ,这意味着案例4的成功概率为 \( \frac{1}{4} \) (因为包含所有可能数对的边界正方形总面积为1)。
将每个案例的成功率相加,我们得到: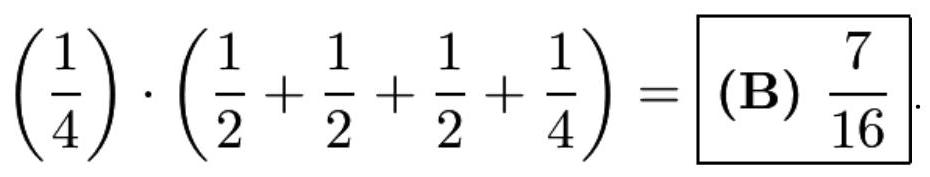
问题
特拉维斯不得不照看令人头疼的汤普森三胞胎。他知道三胞胎喜欢大数字,于是为他们设计了一个数数游戏。首先塔德说数字1,接着托德必须说出接下来的两个数字(2和3),然后塔克必须说出接下来的三个数字(4、5、6),之后塔德必须说出接下来的四个数字(7、8、9、10),如此按顺序轮流由三个孩子继续,每个人比前一个多说一个数字,直到说到数字10,000为止。塔德说出的第2019个数字是多少?
(A) 5743 (B) 5885 (C) 5979 (D) 6001 (E) 6011 解法1 定义一轮(round)为依次经过三个孩子的完整循环。我们制作一张表格,记录每一轮中每个孩子说出的数字。
| 轮次 | 塔德 | 托德 | 塔克 |
| 1 | 1 | 2-3 | 4-6 |
| 2 | 7-10 | 11-15 | 16-21 |
| 3 | 22-28 | 29-36 | 37-45 |
| 4 | 46-55 | 56-66 | 67-78 |
注意,在每一 \( {n}^{\mathrm{{th}}} \) 轮结束时,最后说出的数字是第 \( 3{n}^{\mathrm{{th}}} \) 个三角数(triangular number)。
塔德(Tadd)在第1轮说1个数字,第2轮说4个数字,第3轮说7个数字,一般地,在第 \( n \) 轮说 \( {3n} - 2 \) 个数字。到第 \( n \) 轮结束时,塔德已说出的数字总数为 \( 1 + 4 + 7 + \cdots + \left( {{3n} - 2}\right) = \frac{n\left( {{3n} - 1}\right) }{2} \) ,这由等差数列求和公式得出。
因此,我们要找最小的正整数 \( k \) ,使得 \( {2019} \leq \frac{k\left( {{3k} - 1}\right) }{2} \) 。 \( k \) 的值将告诉我们塔德在哪一轮说出他的第 \( {2019}^{\mathrm{{th}}} \) 个数字。通过试算(或实际解二次不等式), \( k = {37} \) 。
现在,利用我们的公式 \( \frac{n\left( {{3n} - 1}\right) }{2} \) ,塔德在前36轮共说了1926个数字,因此我们要找他在第 \( {37}^{\mathrm{{th}}} \) 轮说出的第 \( \left( {{2019} - {1926}}\right) = {93}^{\mathrm{{rd}}} \) 个数字。
我们发现,在第 \( {n}^{\mathrm{{th}}} \) 轮结束时最后说出的数字是第 \( 3{n}^{\mathrm{{th}}} \) 个三角数。对于 \( n = {36} \) ,第 \( {108}^{\mathrm{{th}}} \) 个三角数是5886。因此答案是 \( {5886} + {93} = {(C)579.} \) 。
解法2
首先,与解法1一样,我们列出塔德、托德(Todd)和塔克(Tucker)在每一轮各说多少个数字。
塔德: \( 1,4,7,{10},{13}\cdots \)
托德: \( 2,5,8,{11},{14}\cdots \)
塔克: \( 3,6,9,{12},{15}\cdots \)
我们可以为每个孩子在第 \( n \) 轮之后说出的数字总数找到一个通式。对塔德,我们既可以用等差数列求和公式(如解法1),也可以用标准求和结果得到
\[ \mathop{\sum }\limits_{{i = 1}}^{n}{3n} - 2 = - {2n} + 3\mathop{\sum }\limits_{{i = 1}}^{n}n = - {2n} + \frac{{3n}\left( {n + 1}\right) }{2} = \frac{3{n}^{2} - n}{2}. \]
现在,为了求塔德和他的兄弟姐妹在塔德说出第2019个数字之前共进行了多少轮,我们知道不等式 \( \frac{3{n}^{2} - n}{2} < {2019} \) 必须成立,试算后得到 \( n \) 的最大整数值为36。
接下来的关键洞察是,为了简化计算,注意到塔德说的第2019个数字其实就是托德和塔克说的数字总数再加上塔德说的2019个数字,由于塔德先开口,这就是最终答案。
因此,计算过程变得非常简单:
\[ \left( {\mathop{\sum }\limits_{{i = 1}}^{{36}}{3n} + \mathop{\sum }\limits_{{i = 1}}^{{36}}{3n} - 1}\right) + {2019} = \left( {\mathop{\sum }\limits_{{i = 1}}^{{36}}{6n} - 1}\right) + {2019} = \left( {5 + {11} + {17}... + {215}}\right) + {2019} = \frac{{36}({220}}{2} \]
此时,我们可以注意到答案的个位数是9,对应选项(C) 5979。(如有时间,完成计算即可验证答案。)
2019 AMC 10A 试题/第24题
问题
设 \( p \) 、 \( q \) 和 \( r \) 为多项式 \( {x}^{3} - {22}{x}^{2} + {80x} - {67} \) 的互不相同的根。已知存在实数 \( A \) 、 \( B \) 和 \( C \) 使得
\[ \frac{1}{{s}^{3} - {22}{s}^{2} + {80s} - {67}} = \frac{A}{s - p} + \frac{B}{s - q} + \frac{C}{s - r} \]
对所有 \( s \notin \{ p, q, r\} \) 成立。 \( \frac{1}{A} + \frac{1}{B} + \frac{1}{C} \) 的值是多少?
(A) 243 (B) 244 (C) 245 (D) 246
解法1
两边同乘 \( \left( {s - p}\right) \left( {s - q}\right) \left( {s - r}\right) \) 得
\[ 1 = A\left( {s - q}\right) \left( {s - r}\right) + B\left( {s - p}\right) \left( {s - r}\right) + C\left( {s - p}\right) \left( {s - q}\right) \]
由于这是一个多项式恒等式,且对无穷多个 \( s \) 成立,故对所有 \( s \) 均成立(因为具有无穷多个根的多项式必为零多项式)。这意味着我们可以代入 \( s = p \) 得到 \( \frac{1}{A} = \left( {p - q}\right) \left( {p - r}\right) \) 。同理可求 \( \frac{1}{B} = \left( {q - p}\right) \left( {q - r}\right) \) 和 \( \frac{1}{C} = \left( {r - p}\right) \left( {r - q}\right) \) 。将它们相加,得到
\[ \frac{1}{A} + \frac{1}{B} + \frac{1}{C} = {p}^{2} + {q}^{2} + {r}^{2} - {pq} - {qr} - {pr} \]
由韦达公式(Vieta's Formulas)可知 \( {p}^{2} + {q}^{2} + {r}^{2} = {\left( p + q + r\right) }^{2} - 2\left( {{pq} + {qr} + {pr}}\right) = {324} \) 且 \( {pq} + {qr} + {pr} = {80} \) 。因此答案为 \( {324} - {80} = \) (B)244。
注:在原恒等式中代入“禁止”值的过程是微积分课程中讲授的部分分式分解(Partial Fraction Decomposition)的标准技巧。
解法2(极限法)
两边同乘(s - p)得
\[ \frac{s - p}{{s}^{3} - {22}{s}^{2} + {80s} - {67}} = A + \frac{B\left( {s - p}\right) }{s - q} + \frac{C\left( {s - p}\right) }{s - r} \]
当 \( s \rightarrow p \) 时,注意右侧的 \( B \) 和 \( C \) 项将抵消,仅剩 \( A \) 。因此
\( A = \mathop{\lim }\limits_{{s \rightarrow p}}\frac{s - p}{{s}^{3} - {22}{s}^{2} + {80s} - {67}} \) ,由洛必达法则(L'Hôpital's Rule)得
\( \mathop{\lim }\limits_{{s \rightarrow p}}\frac{1}{3{s}^{2} - {44s} + {80}} = \frac{1}{3{p}^{2} - {44p} + {80}} \) 。同理可求 \( B \) 和 \( C \) 。将倒数相加并利用韦达公式,得到
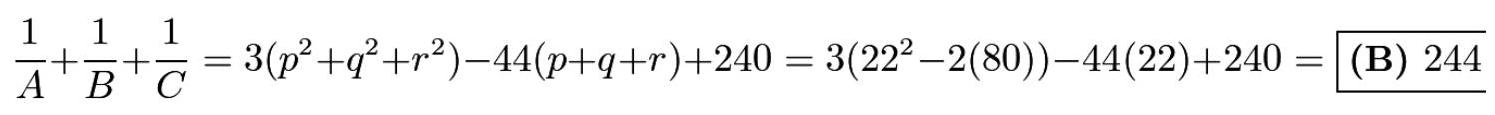
2019 AMC 10A 试题/第25题
问题
在1到50(含)之间有多少个整数 \( n \) 使得
\[ \frac{\left( {{n}^{2} - 1}\right) !}{{\left( n!\right) }^{n}} \]
为整数?(回忆 \( 0! = 1 \) 。)
(A) 31 (B) 32 (C) 33 (D) 34 (E) 35
解法1
关键洞察是
\[ \frac{\left( {n}^{2}\right) !}{{\left( n!\right) }^{n + 1}} \]
恒为整数。这是因为其恰好等于将 \( {n}^{2} \) 个对象划分为 \( n \) 个无序且每组大小为 \( n \) 的组的方式数。因此,
\[ \frac{\left( {{n}^{2} - 1}\right) !}{{\left( n!\right) }^{n}} = \frac{\left( {n}^{2}\right) !}{{\left( n!\right) }^{n + 1}} \cdot \frac{n!}{{n}^{2}} \]
为整数当且仅当 \( {n}^{2} \mid n! \) ,换言之,当且仅当 \( n \mid \left( {n - 1}\right) ! \) 。根据威尔逊定理,该条件不成立当且仅当 \( n = 4 \) 或 \( n \) 为素数。1到50(含)之间有15个素数,因此有 \( {15} + 1 = {16} \) 项使得
\[ \frac{\left( {{n}^{2} - 1}\right) !}{{\left( n!\right) }^{n}} \]
可能不为整数。容易验证,当 \( n = 4 \) 时,上述表达式不为整数,因为分母中2的因子多于分子。类似地,可验证对任意素数 \( n = p \) ,该表达式均不为整数,因为分母中p的因子多于分子。因此,全部16个 \( n \) 值均使表达式不为整数,答案为 \( {50} - {16} = \left( \mathbf{D}\right) {34} \)
解法2
我们可用n的p进赋值(P-Adic Valuation)解决此题(回忆n的p进赋值记作 \( {v}_{p}\left( n\right) \) ,定义为能整除n的素数p的最高次幂。例如, \( {v}_{2}\left( 6\right) = 1 \) 或 \( {v}_{7}\left( {245}\right) = 2 \) 。)利用勒让德公式,我们知道:
\[ {v}_{p}\left( {n!}\right) = \mathop{\sum }\limits_{{i = 1}}^{\infty }\left\lfloor \frac{n}{{p}^{i}}\right\rfloor \]
看到题目中出现阶乘,这提示我们使用勒让德公式,其中 \( n \) 为素数的幂。
我们还知道, \( {v}_{p}\left( {m}^{n}\right) = n \cdot {v}_{p}\left( m\right) \) 。已知若 \( {v}_{p}\left( a\right) \leq {v}_{p}\left( b\right) \) ,则 \( a \mid b \) ,于是我们有:
\[ n \cdot {v}_{p}\left( {n!}\right) \leq {v}_{p}\left( {\left( {{n}^{2} - 1}\right) !}\right) \]
且需找出所有使该式成立的 \( n \) 。
若代入 \( n = p \) ,由勒让德公式可得两个方程:
\[ {v}_{p}\left( {\left( {{n}^{2} - 1}\right) !}\right) = \mathop{\sum }\limits_{{i = 1}}^{\infty }\left\lfloor \frac{{n}^{2} - 1}{{p}^{i}}\right\rfloor = \left( {p - 1}\right) + 0 + \ldots + 0 = p - 1 \]
我们还得到:
\[ {v}_{p}\left( {\left( n!\right) }^{n}\right) = n \cdot {v}_{p}\left( {n!}\right) = n \cdot \mathop{\sum }\limits_{{i = 1}}^{\infty }\left\lfloor \frac{n}{{p}^{i}}\right\rfloor = p \cdot \left( {1 + 0 + \ldots 0}\right) = p \]
但题目要求证明
\( n \cdot {v}_{p}\left( {n!}\right) \leq {v}_{p}\left( {\left( {{n}^{2} - 1}\right) !}\right) \Rightarrow p \leq p - 1 \) 对所有 \( n \) 为假,其中 \( n \) 为素数。
现在我们尝试对 \( n = {p}^{2} \) 做同样的事,其中p为素数。根据勒让德(Legendre)我们得到:
\[ {v}_{p}\left( {\left( {{p}^{4} - 1}\right) !}\right) = {p}^{3} + {p}^{2} + p - 3 \]
并且
\[ {p}^{2} \cdot {v}_{p}\left( {{p}^{2}!}\right) = {p}^{3} + {p}^{2} \]
于是我们得到:
\[ {p}^{2} \cdot {v}_{p}\left( {p!}\right) \leq {v}_{p}\left( {\left( {{n}^{4} - 1}\right) !}\right) \Rightarrow {p}^{3} + {p}^{2} \leq {p}^{3} + {p}^{2} + p - 3 \]
这对所有素数都成立,除了2,因此 \( {2}^{2} = 4 \) 不成立。可以轻易验证,对所有 \( n = {p}^{i} \) ,其中 \( i \) 为大于2的整数,满足不等式:
\[ n \cdot {v}_{p}\left( {n!}\right) \leq {v}_{p}\left( {\left( {{n}^{2} - 1}\right) !}\right) \]
